树状数组简介

引入问题

给出一个长度为 \(n\) 的数组，完成以下两种操作：

1. 将第 \(i\) 个数加上 \(k\)
2. 输出区间 \([i,j]\) 内每个数的和

朴素算法

• 单点修改：\(O(1)\)
• 区间查询：\(O(n)\)

使用树状数组

• 单点修改：\(O(\log n)\)
• 区间查询：\(O(\log n)\)

前置知识

lowbit()运算：非负整数 \(x\) 在二进制表示下最低位 \(1\) 及其后面的 \(0\) 构成的数值。

举例说明：

\(lowbit(12)=lowbit([1100]_2)=[100]_2=4\)

函数实现：

int lowbit(int x) {
    return x & -x;
}

---

树状数组思想

树状数组的本质思想是使用树结构维护前缀和，从而把时间复杂度降为 \(O(\log n)\)。

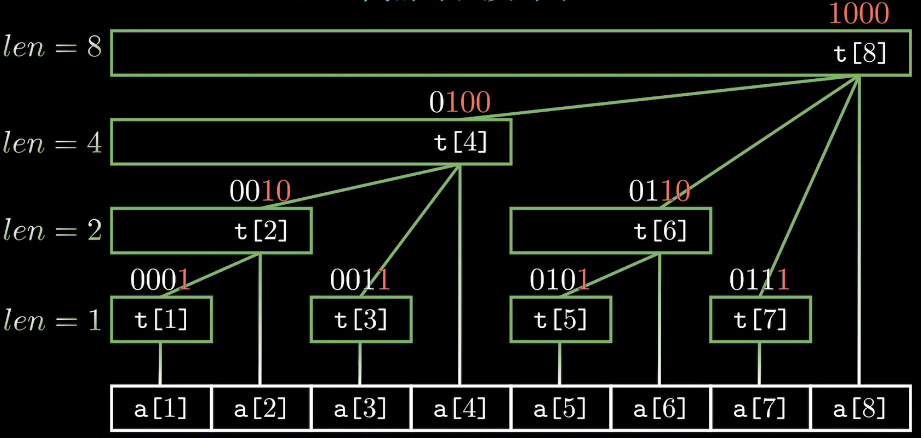
对于一个序列，对其建立如下树形结构：

1. 每个结点 \(tr[x]\) 保存以 \(x\) 为根的子树中叶结点值的和；
2. 每个结点覆盖的长度为 \(lowbit(x)\)；
3. \(tr[x]\) 结点的父结点为 \(tr[x + lowbit(x)]\)；
4. 树的深度为 \(\log_2{n}+1\)。

---

树状数组操作

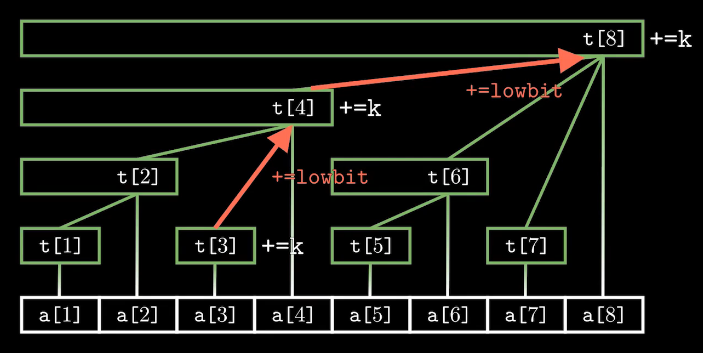
add(x, k)表示将序列中第x个数加上k

以 add(3, 5) 为例：

在整棵树上维护这个值，需要一层一层向上找到父结点，并将这些结点上的 \(tr[x]\) 值都加上 \(k\)，这样保证计算区间和时的结果正确。时间复杂度为 \(O(\log n)\)。

void add(int x, int k) {
    for (int i = x; i <= n; i += lowbit(i))
        tr[i] += k;
}

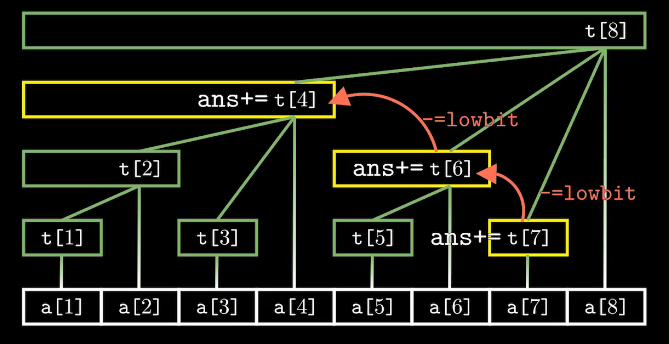
sum(x) 表示将查询序列前x个数的和

以 sum(7) 为例：

查询这个点的前缀和，需要从这个点向左上找到上一个结点，将加上其结点的值。向左上找到上一个结点，只需要将下标 \(x -= lowbit(x)\)，例如 \(7 - lowbit(7) = 6\)。

int sum(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

---

总结

树状数组三大核心操作：

• lowbit(x) 求非负整数 \(x\) 在二进制表示下最低位 \(1\)
• add(x, k) 在第x个位置上加上k
• sum(x) 求第1~x个元素的和

在 c/c++ 中，为了解决一些频繁调用的小函数大量消耗栈空间（栈内存）的问题，特别的引入了 inline 修饰符，表示为内联函数。

inline int lowbit(int x) {
    return x & (-x);
}

inline void add(int x, int k) {
    for (int i = x; i <= n; i += lowbit(i))
        tr[i] += k;
}

inline int sum(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}