配对统计(GZOI2017)

原题链接

题目详情

数据范围

• \(1 \le n,m \le 300000\)
• \(1 \le a_i \le 10^9\)
• \(i \ne j,a_i \ne a_j\)

---

算法与思路

寻找所有好对

首先我们来理解题意：

\(\left\vert a_x-a_y\right\vert \le \left\vert a_x-a_i\right\vert(i\ne x)\) ，就是说 \(a_x\) 和 \(a_y\) 对于 \(a_x\) 是相差最小两个数，放到数轴上就是挨得最近的两个数。

所以就想到了排序，这样每个数可能的好对就是它和它两边的两个数。

举个例子：

\[3,9,11,4,8,6\]

编号

\[1,2,3,4,5,6\]

排序过后就变成

\[3,4,6,8,9,11\]

对应的编号是

\[1,4,6,5,2,3\]

对于每一个数，判断一下它与它左右两边的数的差的绝对值：

如果相等，那么就是两个好的配对（左右两边都是好对），以6为例：

\(\left\vert 6-4\right\vert = \left\vert 6-8\right\vert\) \(6\) 和 \(4\) 对应的好对为 \((6,4)\)，\(6\) 和 \(8\) 对应的好对为 \((6,5)\)。

如果不相等，那么只有绝对值之差更小的一对，以 \(4\) 为例：

\(\left\vert 4-3\right\vert < \left\vert 4-6\right\vert\) 只有 \(4\) 和 \(3\) 的好对 \((4,1)\) 。

当然两边的数只有唯一的一对

要注意的是，如果一个配对 \((x,y)\) 是好对， \((y,x)\) 不一定是好对，如9和11： \((3,2)\) 是好对，而 \((2,3)\) 就不是。

数据约束中说到当 \(i \ne j,a_i \ne a_j\)，即 \(a\) 中没有相同的元素，这样就保证了这个配对判断的正确性。

至此我们已经找到了所有的配对，时间复杂度 \(O(n \log n)\) （瓶颈在排序）。

查询所有询问

对于每次查询，我们只把右端点在 \((0,r]\) 内的好对放进树状数组。

树状数组 \(tr[i]\) 表示左端点在 \([i-\operatorname{lowbit}(i)+1 , i]\) 内的所有好对的的个数。

已经放入的好对个数，减去左端点在 \((0,l-1]\) 内的好对（也就是减去 \(\operatorname{query}(l-1)\) ），就可以得到答案了。

举个例子：

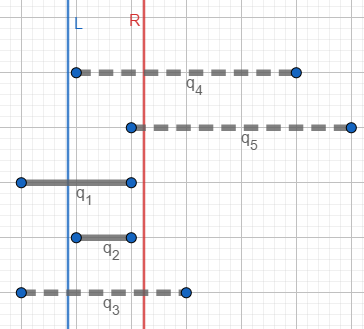
实线表示该好对在树状数组中，虚线表示该好对还未放入树状数组。

待查询的区间 \([L,R]\) 如图所示，此时只有 \(q_1,q_2\) 两个好对在R左侧，再减去左端点在L左侧的 \(q_1\) ，就得到 \([L,R]\) 内的好对数目：1个（ \(q_2\) ）。

我们再将所有的好对和所有的询问，都按右端点从小到大排个序。

每次R右移，就将右端点小于等于R的所有好对，都加入到树状数组里，再减去左端点在 \((0,l-1]\) 内的好对个数就是答案。

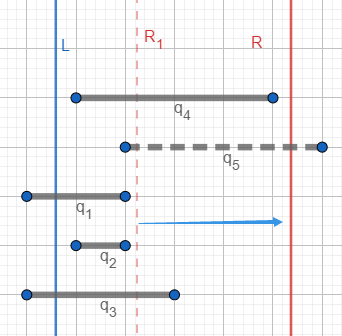
此时R右移， \(q_3,q_4\)被放入树状数组，再减去左端点在L左侧的 \(q_1,q_3\)，就得到 \([L,R]\) 内的好对数目：2个（\(q_2,q_4\)）。

遍历每个询问\(O(n)\)，每次查询\(O(\log n)\),总时间复杂度\(O(n \log n)\)。

统计答案

因为答案的计算方法很特殊， \(\sum_{i=1}^mAns_i \times i\)

所以我们在给询问排序的时候也要记录下它原先的 \(i\) （代码中为 \(pos\) ）。

\(Ans_i\)的计算方法上文已经讲得很清楚了，这里不再多说。

整体时间复杂度 \(O(n \log n)\) 。

---

代码

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;

const int N = 300010;

int n, m, tot;
int tr[N];
struct node {
    int val, id;
    bool operator < (const node &t) const {
        return val < t.val;
    }
} w[N];

struct match {
    int l, r;
    bool operator < (const match &t) const {
        if (r != t.r) return r < t.r;
        return l < t.l;
    }
} p[N << 1];

struct query {
    int l, r, id;
    bool operator < (const query &t) const {
        if (r != t.r) return r < t.r;
        return l < t.l;
    }
} q[N];

void add_match(node a, node b) {
    int l = min(a.id, b.id);
    int r = max(a.id, b.id);
    p[++tot] = {l, r};
}

inline int lowbit(int x) {
    return x & -x;
}

inline void add(int x, int k) {
    for (int i = x; i <= n; i += lowbit(i))
        tr[i] += k;
}

inline i64 sum(int x) {
    i64 res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> w[i].val;
        w[i].id = i;
    }

    if (n == 1) {
        cout << "0\n";
        return 0;
    }

    sort(w + 1, w + 1 + n);

    add_match(w[1], w[2]);
    add_match(w[n], w[n - 1]);
    for (int i = 2; i < n; i++) {
        int diff1 = w[i].val - w[i - 1].val;
        int diff2 = w[i + 1].val - w[i].val;
        if (diff1 < diff2) add_match(w[i], w[i - 1]);
        else if (diff1 > diff2) add_match(w[i + 1], w[i]);
        else {
            add_match(w[i], w[i - 1]);
            add_match(w[i], w[i + 1]);
        }
    }

    sort(p + 1, p + 1 + tot);

    for (int i = 1; i <= m; i++) {
        int l, r;
        cin >> l >> r;
        q[i] = {l, r, i};
    }

    sort(q + 1, q + 1 + m);

    i64 res = 0;
    for (int i = 1, j = 1; i <= m; i++) {
        while (j <= tot && p[j].r <= q[i].r) {
            add(p[j].l, 1);
            j++;
        }
        res += (sum(q[i].r) - sum(q[i].l - 1)) * q[i].id;
    }

    cout << res << '\n';

    return 0;
}

运行结果