跳转至

食物链(NOI2001)

原题链接

题目详情

swl

数据范围

  • \(1\le N\le 5\times 10^4\)
  • \(1\le K\le 10^5\)

算法与思路

对于询问是否在同一类或者不同类之间关系的题目，可以用并查集来维护。

对于A，B，C三种动物，可以通过维护与父节点的距离 d[] 来判断同类或捕食关系。即：

  • 当动物 \(x\) 和动物 \(y\) 的距离 \(\bmod3\) 等于 \(1\) 时,说明 \(x\) 捕食 \(y\)；
  • 当动物 \(x\) 和动物 \(y\) 的距离 \(\bmod3\) 等于 \(2\) 时,说明 \(y\) 捕食 \(x\)；
  • 当动物 \(x\) 和动物 \(y\) 的距离 \(\bmod3\) 等于 \(0\) 时,说明 \(x\) 和 \(y\) 是同类。

如何判断假话

情况(1) x，y 不在编号内
\[(x>n) \lor (y>n)\]
情况(2) x 与 y 是同类，但是 x 吃 y

因为合并 \(x\) 和 \(y\) 所在集合多出了一段长度

这块长度是 \(find(x)\) 到 \(find(y)\) 的距离

所以求多出来的这块部分的长度

当 \(x\) 和 \(y\) 是同类时,有这样的特性

\((len[x]+len[find[x]]-len[y])\bmod 3\equiv 0\)

这里的 \(len[x]\) 是还未合并时, \(x\) 到 \(find[x]\) 的距离

\(\therefore len[find[x]]=len[y]-len[x]\)

情况(3) x 吃 y，但是 x 与 y 是同类

  • 当 \(x\) 和 \(y\) 在一个集合中时，且 \(x\) 捕食 \(y\)，则

    \(x\) 到根节点的距离 - \(y\) 到根节点的距离 = \(1+3k\), \(k\)为任意实数

    \(\therefore\) 当 \((len[x]-len[y]-1-3k)\bmod 3\equiv 0\) 时可确认 \(x\) 捕食 \(y\)

  • 当 \(x\) 和 \(y\) 不在同一集合时，设 \(find(x)\) 到 \(find(y)\) 的距离为 \(len([find(x)])\)

    此时有 \(len[x]+len([find(x)])-len[y]=3k+1\)

    \(\therefore len[find(x)]=-len[x]+len[y]+1+3k\)

对于d[i]真正的含义及 find() 函数调用过程

img

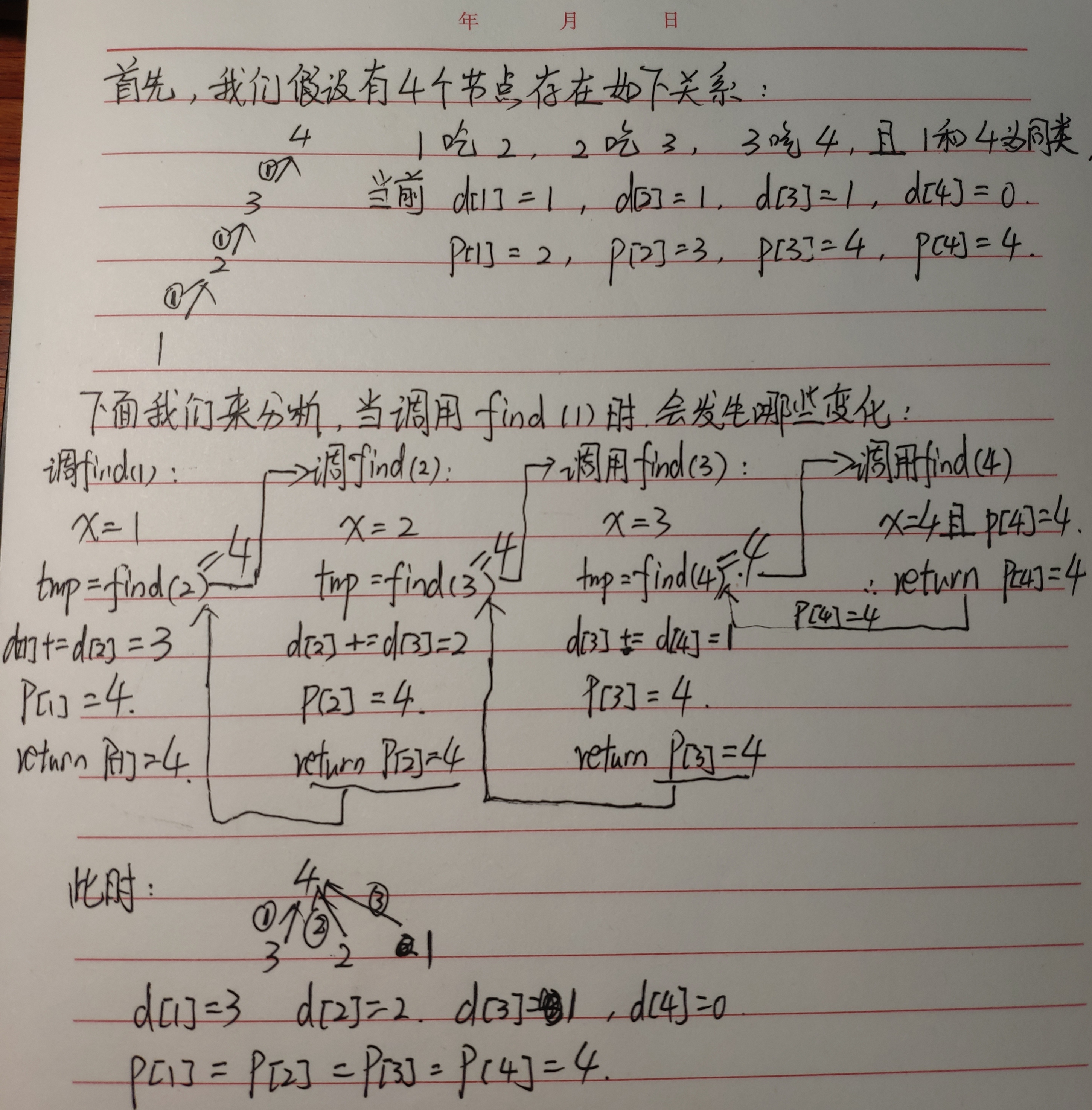
代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <bits/stdc++.h>
using i64 = long long;

const i64 N = 50010;

i64 n, m;
i64 p[N], d[N];

i64 find(i64 x) {
    if (p[x] != x) {
        i64 t = find(p[x]);
        d[x] += d[p[x]];
        p[x] = t;
    }
    return p[x];
}

void solve() {
    std::cin >> n >> m;

    for (i64 i = 1; i <= n; i++) p[i] = i;

    i64 res = 0;
    while (m--) {
        i64 op, x, y;
        std::cin >> op >> x >> y;

        if (x > n || y > n) res++;  // 情况1
        else {
            i64 pa = find(x), pb = find(y);
            if (op == 1) {
                if (pa == pb && (d[x] - d[y]) % 3) res++;   // 情况2
                else if (pa != pb) {
                    p[pa] = pb;
                    d[pa] = d[y] - d[x];
                }
            } else {
                if (pa == pb && (d[x] - d[y] - 1) % 3) res++;   // 情况3
                else if (pa != pb) {
                    p[pa] = pb;
                    d[pa] = d[y] + 1 - d[x];
                }
            }
        }
    }

    std::cout << res << '\n';
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    solve();

    return 0;
}

运行结果

accept

回到页面顶部