17.21. 直方图的水量

原题链接

题目描述

给定一个直方图(也称柱状图)，假设有人从上面源源不断地倒水，最后直方图能存多少水量?直方图的宽度为 1。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的直方图，在这种情况下，可以接 6 个单位的水（蓝色部分表示水）。 

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

---

算法与思路

双指针   \(O(n)\)

如果可以盛水，则要求左右两边均有高于当前柱子的柱子。

盛水量根据 木桶效应 取决于左右两边较矮的那根柱子。

定义当前柱子高度为 \(height[i]\)，左边最高的柱子为 \(left[i]\)，右边最高柱子为 \(right[i]\)，则储水量为 \(min(left[i], right[i]) - height[i]\)。

可以保证结果不为负数，因为 \(left[i]\) 与 \(right[i]\) 始终 大于或等于 当前柱子 \(height[i]\)。

---

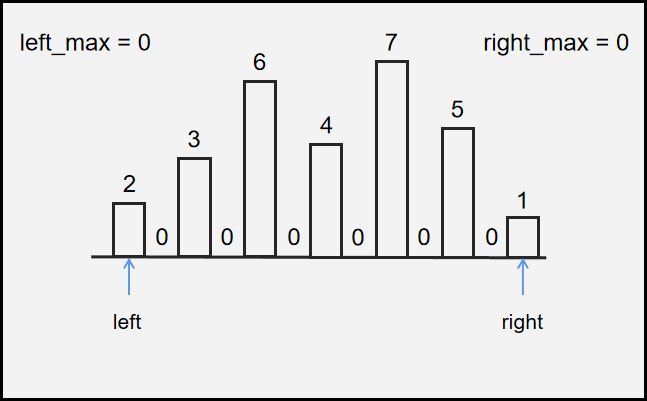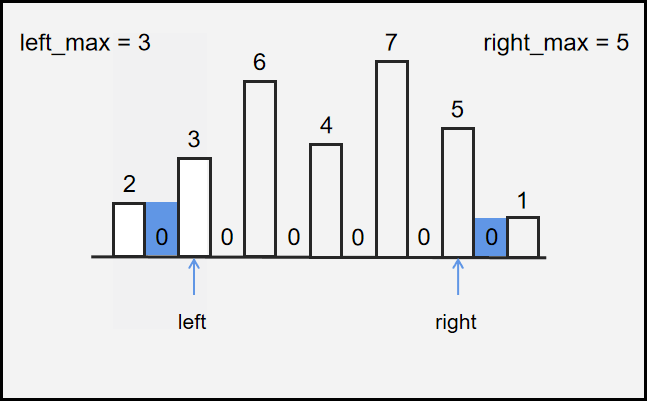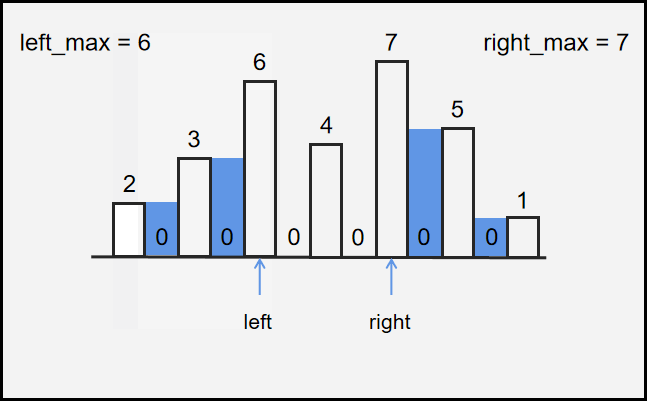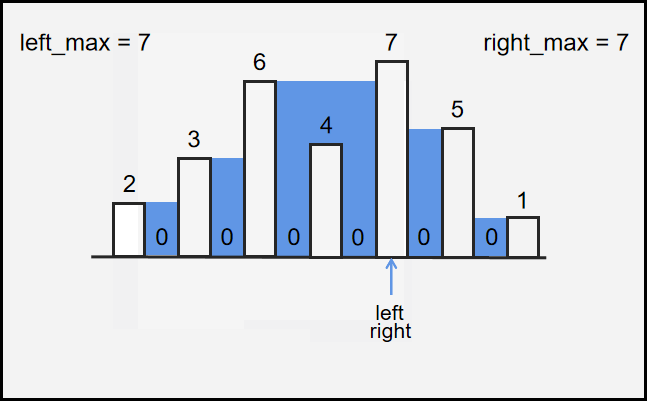
代码

C++

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.empty()) return 0;   // 若没有柱子，返回0

        int n = height.size();
        vector<int> left(n), right(n);
        left[0] = height[0], right[n - 1] = height[n - 1];
        for (int i = 1; i < n; i++)
            left[i] = max(left[i - 1], height[i]);
        for (int i = n - 2; i >= 0; i--)
            right[i] = max(right[i + 1], height[i]);

        int res = 0;
        for (int i = 0; i < n; i++)
            res += min(left[i], right[i]) - height[i];
        return res;
    }
};