跳转至

最大数(单点修改，区间查询)

原题链接

题目简述

给定一个正整数数列 \(a_1,a_2,…,a_n\)，每一个数都在 \(0∼p−1\) 之间。

可以对这列数进行两种操作：

  1. 添加操作：向序列后添加一个数，序列长度变成 \(n+1\)；
  2. 询问操作：询问这个序列中最后 \(L\) 个数中最大的数是多少。 程序运行的最开始，整数序列为空。

一共要对整数序列进行 \(m\) 次操作。

写一个程序，读入操作的序列，并输出询问操作的答案。

其他要求

题目描述

详情请见原题

算法与思路   线段树

首先，确定线段树节点所包含的信息。题目要求区间内的最大值，因此线段树节点必须包含一个数 \(v\) 来表示最大值。 

1
2
3
4
struct node {
    int l, r;
    int v;  // 区间[l, r]的最大值
} tr[N * 4];
现在需要考虑，如果节点仅包含 \(v\)，父节点是否能从左右子节点中得出答案？即得出当前节点的区间内的最大值。

答案是可以的。设当前父节点的区间为 \([l, r]\)，则左儿子节点的区间为 \([l, mid]\)，右儿子节点区间为 \([mid + 1, r]\)，其中 \(mid=⌊\frac{l + r}{2}⌋\)。那么可以很自然的得出，父节点的最大值必然一定存在于区间 \([l, r]\)中，而左右儿子节点所在区间 \([l, mid]\) 和 \([mid + 1, r]\) 正好不重不漏的覆盖住了父节点区间，因此 父节点区间内最大值=\(max\)(左儿子节点区间内最大值, 右儿子区间内最大值)

可以根据以上分析写出向上转移函数 pushup(int u): 

1
2
3
void pushup(int u) {
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}

由于题目描述：

向序列后面加一个数，加入的数是 \((t+a)\) \(mod\) \(p\)。其中，\(t\) 是输入的参数，\(a\) 是在这个添加操作之前最后一个询问操作的答案（如果之前没有询问操作，则 \(a=0\)）。

建树操作：

线段树的插入删除操作非常麻烦，而修改操作较为简单，因此在建树的时候，可以先把整颗树建立起来，最多总共可能有 \(m\) 个数，因此建立一个区间为 \([1, m]\) 的线段树。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
int main() {
    int n = 0, last = 0;
    cin >> m >> p;
    build(1, 1, m); // 从父节点u，区间[1, m]的范围开始建树

    char op;
    int x;
    while (m--) {
        cin >> op >> x;
        ......
    }
}

查询操作：

这个题目是一个动态插入的过程，即不能使用RMQ此类静态算法来解决。我们需要额外定义一个 \(int\) 型整数 \(last\) 来存储上一次询问得到的答案。从 \(1\) 号节点开始查询，目标区间为 \([n - t + 1, n]\)。

1
2
3
4
if (op == 'Q') {    // 查询
    last = query(1, n - t + 1, n);
    cout << last << endl;
}

插入操作：

额外定义一个 \(int\) 型整数 \(n\) ，用来存储当前已插入了几个数。由于 \(t\) 最大为 \(2*10^9\)，并且 \(last\) 最大也为 \(2*10^9\)，相加后可以到达 \(4*10^9\)，超过了 \(int_{max}\)，需要强制转化为 \(long\ long\)。最后再把记录已插入的数 \(+1\)，即 n++。 

1
2
3
4
if (op == 'A') {    // 插入(其实可以认为是修改)
    modify(1, n + 1, (1ll * t + last) % p);
    n++;
}

完善函数

build(int u, int l, int r)
1
2
3
4
5
6
7
void build(int u, int l, int r) {   // 以u为根节点，维护区间[l, r]
    tr[u] = {l, r};                 // 当前节点u的区间设为[l, r]
    if (l == r) return;             // 已经是叶子结点了
    int mid = l + r >> 1;
    build(u << 1, l, mid);          // 左儿子
    build(u << 1 | 1, mid + 1, r);  // 右儿子
}
query(int u, int l, int r)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int query(int u, int l, int r) {    // 从u结点开始，查找区间[l, r]的信息 
    // 1. 不必分治，直接返回
    //      Tl-----Tr
    //   L-------------R  
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;

    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;

    // 2. 需要在tr的左区间[Tl, m]继续分治
    //     Tl----m----Tr
    //        L-------------R 
    if (l <= mid) v = query(u << 1, l, r);

    // 3. 需要在tr的右区间(m, Tr]继续分治
    //     Tl----m----Tr
    //   L---------R 
    if (r > mid) v = max(v, query(u << 1 | 1, l, r));

    // (2)(3)涵盖了这种情况
    //     Tl----m----Tr
    //        L-----R 
    return v;
}
modify(int u, int x, int v)
1
2
3
4
5
6
7
8
9
void modify(int u, int x, int v) {  // 从u结点开始查找，找到编号为x的结点，把值修改为v
    if (tr[u].l == x && tr[u].r == x) tr[u].v = v;  // 找到了
    else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v); // x在左半区间，修改左子树
        else modify(u << 1 | 1, x, v);      // x在右半区间，修改右子树
        pushup(u);  // 更新父节点的信息
    }
}
具体转移流程

区间查询

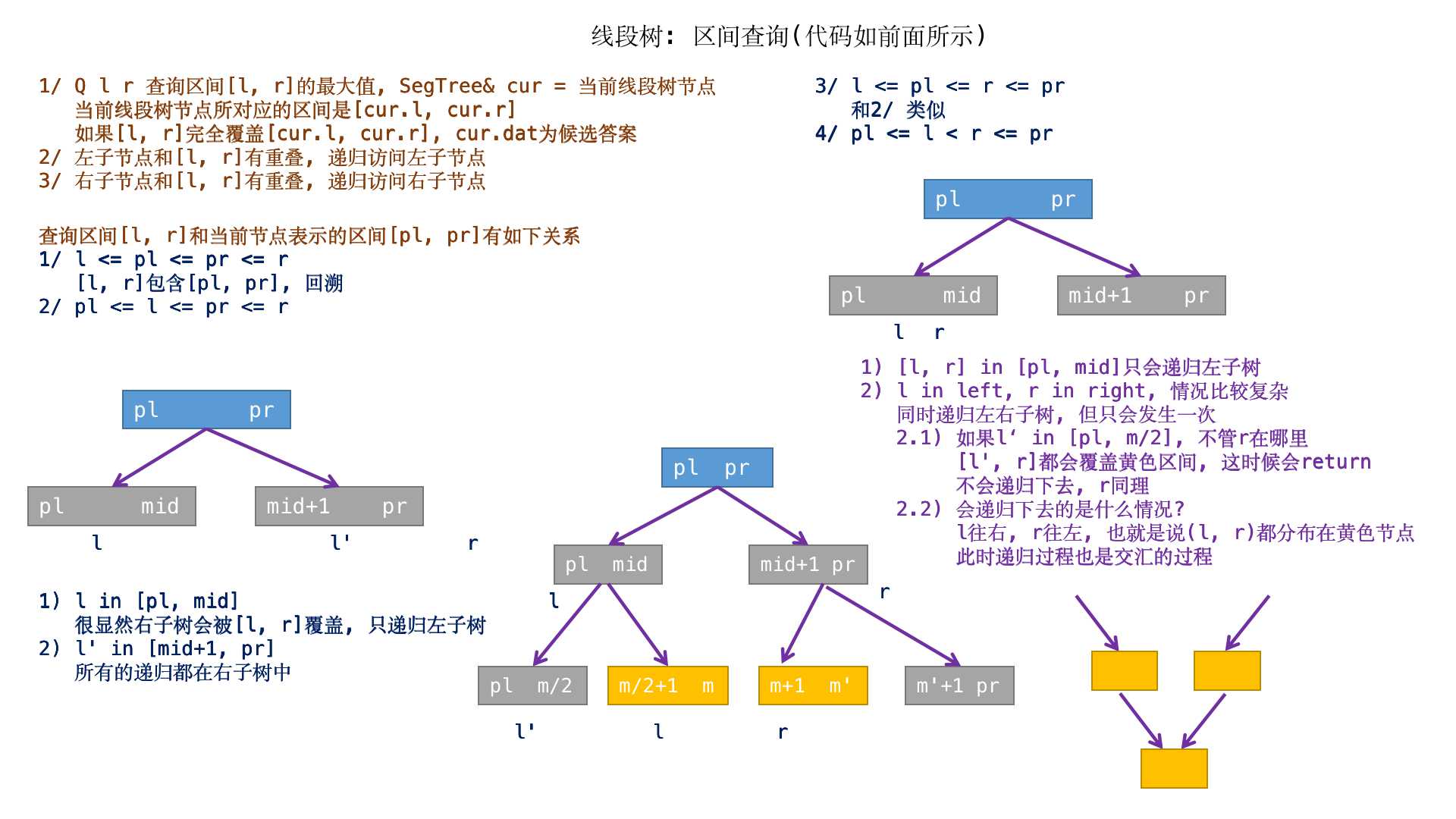
代码 (无注释)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <bits/stdc++.h>
using namespace std;

const int N = 200010;

int m, p;
struct node {
    int l, r;
    int v; 
} tr[N * 4];

void pushup(int u) {
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}

void build(int u, int l, int r) {   
    tr[u] = {l, r};
    if (l == r) return; 
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
}

void modify(int u, int x, int v) { 
    if (tr[u].l == x && tr[u].r == x) tr[u].v = v;
    else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u); 
    }
}

int query(int u, int l, int r) { 
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;

    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if (l <= mid) v = query(u << 1, l, r);
    if (r > mid) v = max(v, query(u << 1 | 1, l, r));
    return v;
}

int main() {
    int n = 0, last = 0;
    cin >> m >> p;
    build(1, 1, m);

    char op;
    int x;
    while (m--) {
        cin >> op >> x;
        if (op == 'A') {
            modify(1, n + 1, (1ll * x + last) % p); 
            n++;
        } else {
            last = query(1, n - x + 1, n); 
            cout << last << endl;
        }
    }

    return 0;
}

运行结果

accept

回到页面顶部