Can you answer these queries III(单点修改,区间查询)
原题链接
题目描述

题目翻译
给定长度为 \(N\) 的数列 \(A\),以及 \(M\) 条指令,每条指令可能是以下两种之一:
\[\max_{x \le l \le r \le y}\sum_{i = l}^r A[i]\]
对于每个查询指令,输出一个整数表示答案。
数据范围
- \(N≤500000,M≤500000\)
- \(−10000≤A[i],\ y≤10000\)
算法与思路
首先,确定线段树节点所包含的信息。要求区间内最大连续子段和,因此线段树节点中必须要有一个数 \(tmax\) 用来存储当前区间 \([l, r]\) 的最大连续字段和。
考虑子节点向父节点转移,单独有 \(tmax\) 并不够。当父节点的最大连续子段和是跨越左右子节点时,并不能保证可以直接由 \(tmax\) 转移过来。
此时我们需要左子节点的最大后缀和 {\(rmax\)} 以及右子节点的最大前缀和 {\(lmax\)}。
由于左右子节点互相独立,因此向父节点转移的 \(tmax\) 无非是以下三种情况:
- 左子节点的最大连续子段和 \(l.tmax\);
- 右子节点的最大连续子段和 \(r.tmax\);
- 左子节点的最大后缀和 {\(l.rmax\)} + 右子节点的最大前缀和 {\(r.lmax\)}。
父节点 \(u.tmax\) 即为:
\[u.tmax = max(l.rmax + r.lmax,\ max(l.tmax,\ r.tmax));\]
那么父节点的 \(lmax\) 和 \(rmax\) 是否可以通过当前已知信息直接转移呢?答案是不能。
父节点的最大前缀和 \(lmax\) 可能会是以下两种情况:
- 左子节点的最大前缀和 \(l.lmax\);
- 左子节点的全部元素和 \(\sum_{i=l}^{mid} A[i]\) + 右子节点的最大前缀和 \(r.lmax\)。
即
\[u.lmax=max(l.lmax,\ l.sum+r.lmax);\]
同理,父节点的最大后缀和的两种情况为:
- 右子节点的最大后缀和 \(r.rmax\);
- 右子节点的全部元素和 \(\sum_{i=mid+1}^{r} A[i]\) + 左子节点的最大后缀和 \(l.rmax\)。
即
\[u.rmax=max(r.rmax,\ r.sum+l.rmax);\]
由上述可见,我们还需要一个 \(sum\) 来存储当前节点区间内所有元素的和。而父节点的 \(sum\) 可以直接由左右子节点的 \(sum\) 计算得出。
即
\[u.sum=l.sum+r.sum;\]
线段树节点 \(node\)
| /************************************
* sum : sum of [l, r] *
* lmax: 最大前缀和 *
* rmax: 最大后缀和 *
* tmax: 区间[l, r]最大连续子段和 *
************************************/
struct node {
int l, r;
int sum, lmax, rmax, tmax;
} tr[N * 4];
|
pushup操作
| void pushup(node &u, node &l, node &r) {
u.sum = l.sum + r.sum;
u.lmax = max(l.lmax, l.sum + r.lmax);
u.rmax = max(r.rmax, r.sum + l.rmax);
u.tmax = max(l.rmax + r.lmax, max(l.tmax, r.tmax));
}
void pushup(int u) {
pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
|
这里使用了重载函数操作,简洁代码。
建树操作
回到最初题目要求,建立一颗区间为 \([1,n]\) 的线段树。
当 \(l=r\) 时,题目要求该区间内至少含有一个数(\(l \le r\)),因此当前节点的 \(tmax, lmax, rmax, sum\) 都为 \(A[r]\)。
- \(tr[u].l = l;\)
- \(tr[u].r = r;\)
- \(tr[u].lmax = tr[u].rmax = tr[u].tmax = tr[u].sum = w[r];\)
同时,也要注意,每次递归完左右子节点后,要将当前父节点的信息修改,即 执行 pushup(u) 操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 | void build(int u, int l, int r) {
if (l == r) tr[u] = {l, r, w[r], w[r], w[r], w[r]}; // 找到叶子节点
else {
tr[u] = {l, r}; // 设当前节点区间为[l, r]
int mid = l + r >> 1;
build(u << 1, l, mid); // 建立左子树
build(u << 1 | 1, mid + 1, r); // 建立右子树
pushup(u); // 修改父节点
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> w[i];
build(1, 1, n);
cin >> m;
int op, x, y;
while (m--) {
cin >> op >> x >> y;
if (op == 0) {
// 修改
} else {
// 查询
}
}
return 0;
}
|
修改操作
每次从 \(1\) 号节点开始找,找到位置位于 \(x\) 的数,把它修改为 \(v\)。
设已找到位于 \(x\) 处的节点,记为 \(tr[u]\)。
易得知当前区间即为 \([x,x]\),题目要求该区间内至少含有一个数(\(l \le r\)),修改 \(A[x]=y\),因此当前节点的 \(tmax, lmax, rmax, sum\) 都为 \(v=y=A[x]\)。
- \(tr[u].l = tr[u].r = x;\)
- \(tr[u].lmax = tr[u].rmax = tr[u].tmax = tr[u].sum = v;\)
| void modify(int u, int x, int v) {
if (tr[u].l == x && tr[u].r == x) tr[u] = {x, x, v, v, v, v}; // 找到了
else {
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) modify(u << 1, x, v); // x位于当前区间的左半子区间
else modify(u << 1 | 1, x, v); // x位于当前区间的右半子区间
pushup(u); // 修改父节点的相关信息
}
}
|
查询操作
查询的时候我们会遇到四种情况。
-
当前节点区间被 \([l,r]\) 所包含,即返回当前节点的信息 return tr[u];
-
查询的区间在当前节点的左半区间 (\(r \le mid\)),
递归搜索左子树,即 query(u << 1, l, r);
-
查询的区间在当前节点的右半区间 (\(l > mid\)),
递归搜索右子树,即 query(u << 1 | 1, l, r);
-
查询的区间横跨左右区间,递归搜索左子树和右子树,最后将搜索得到的 \(left\) 和 \(right\) 子树的信息合并,得到当前节点 \(res\) 的信息,即 pushup(res, left, right);,最后返回 \(res\) 即可。
由上述可知,query函数不能单单只返回一个 \(int\) 型变量,应该返回整个节点的信息,所以定义query函数的返回类型为 \(node\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 | node query(int u, int l, int r) { // 从节点u开始,查找区间[l, r]的信息
// 1. 包含在区间内
// Tl-----Tr
// L-------------R
if (tr[u].l >= l && tr[u].r <= r) return tr[u];
int mid = tr[u].l + tr[u].r >> 1;
// 2. 在当前的左半区间
// Tl-----m-----Tr
// L---R
if (r <= mid) return query(u << 1, l, r);
// 3. 在当前的右半区间
// Tl-----m-----Tr
// L-----R
else if (l > mid) return query(u << 1 | 1, l, r);
// 4. 两边都有,都查询
// Tl----m----Tr
// L-----R
else {
auto left = query(u << 1, l, r);
auto right = query(u << 1 | 1, l, r);
node res;
// 合并答案
pushup(res, left, right);
return res;
}
}
|
具体转移流程
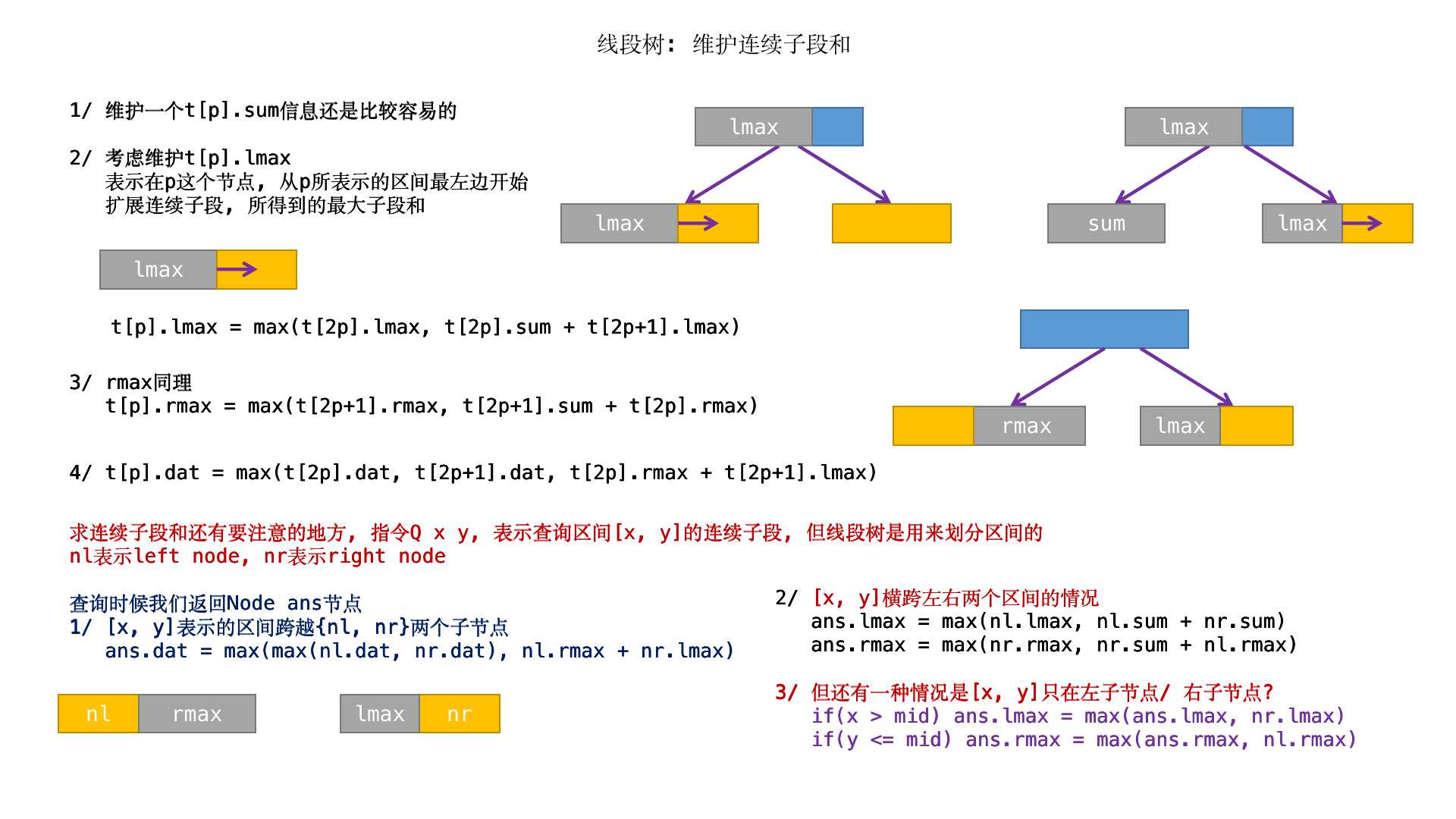
代码(无注释)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78 | #include <bits/stdc++.h>
using namespace std;
const int N = 500010;
int n, m;
int w[N];
struct node {
int l, r;
int tmax, lmax, rmax, sum;
} tr[N * 4];
void pushup(node &u, node &l, node &r) {
u.sum = l.sum + r.sum;
u.lmax = max(l.lmax, l.sum + r.lmax);
u.rmax = max(r.rmax, r.sum + l.rmax);
u.tmax = max(l.rmax + r.lmax, max(l.tmax, r.tmax));
}
void pushup(int u) {
pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
void build(int u, int l, int r) {
if (l == r) tr[u] = {l, r, w[r], w[r], w[r], w[r]};
else {
tr[u] = {l, r};
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void modify(int u, int x, int v) {
if (tr[u].l == x && tr[u].r == x) tr[u] = {x, x, v, v, v, v};
else {
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) modify(u << 1, x, v);
else modify(u << 1 | 1, x, v);
pushup(u);
}
}
node query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u];
int mid = tr[u].l + tr[u].r >> 1;
if (r <= mid) return query(u << 1, l, r);
else if (l > mid) return query(u << 1 | 1, l, r);
else {
auto left = query(u << 1, l, r);
auto right = query(u << 1 | 1, l, r);
node res;
pushup(res, left, right);
return res;
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> w[i];
build(1, 1, n);
cin >> m;
int op, x, y;
while (m--) {
cin >> op >> x >> y;
if (op == 0) {
modify(1, x, y);
} else {
cout << query(1, x, y).tmax << endl;
}
}
return 0;
}
|
运行结果



