旅行问题

原题链接

题目描述

John 打算驾驶一辆汽车周游一个环形公路。

公路上总共有 n 个车站，每站都有若干升汽油（有的站可能油量为零），每升油可以让汽车行驶一千米。

John 必须从某个车站出发，一直按顺时针（或逆时针）方向走遍所有的车站，并回到起点。

在一开始的时候，汽车内油量为零，John 每到一个车站就把该站所有的油都带上（起点站亦是如此），行驶过程中不能出现没有油的情况。

任务：判断以每个车站为起点能否按条件成功周游一周。

---

思路 破环成链+前缀和+单调队列

对于环路，我们需要破环成链，即开两倍的数组，对前n个数字进行复制。

定义： \(d[i]\) 为当前点获得的油量 \(oil[i]\) + 到下一个点的距离 \(dist[i(i - 1)]\)。 \(s[i]=\sum_{j=1}^i d[j]\) 。

顺时针

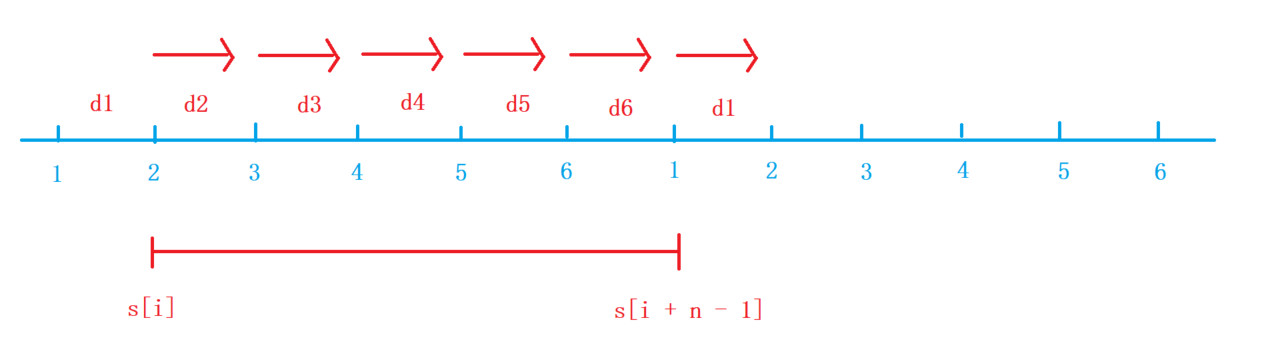
对于顺时针，我们需要满足从 \(i\) 点开始，走到 \(i+n\) 点，油量始终大于等于0。

考虑从 \(i\) 点走向 \(i+1\) 点时的情况，即 \(d[i]=s[i]-s[i-1]=oil[i]-dist[i]\ge 0\)。

由此可以推出，走到 \(i+x_{(0\le x\le n)}\) 点时，需要满足 \(s[i+x]-s[i-1] \ge 0\)。

从而转化为，在区间 \([i,i+n]\) 内找到最小值，满足 \(\min\{s[i,i+n]\}\ge s[i-1]\)。寻找区间里最小值可以用滑动窗口来维护。

Note

此时 \(s[i]\) 需要与 \(s[i-1]\) 进行对比，因此需要先将 \(s[i]\) 放入单调队列后，再进行答案的维护。

逆时针

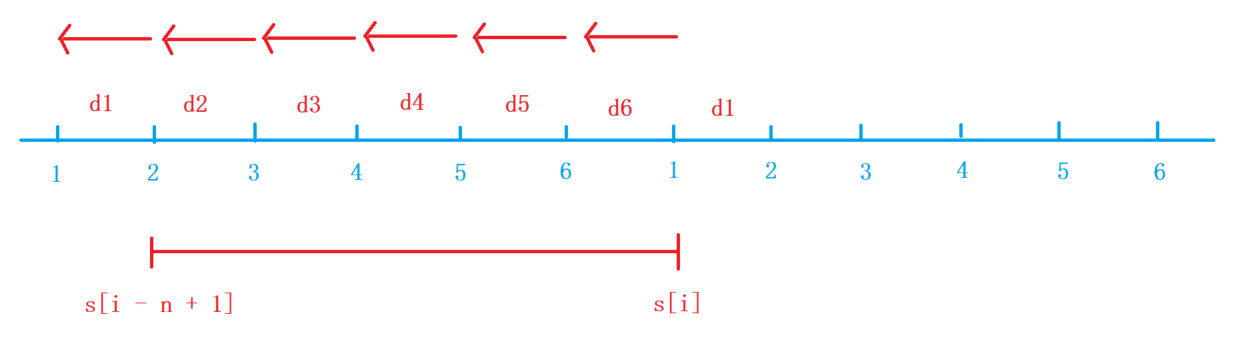
对于逆时针，我们需要满足从 \(i+n\) 点开始，走到 \(i\) 点，油量始终大于等于0。

此时的 \(d[i]=oil[i]-dist[i-1]\)。考虑从 \(i\) 点走向 \(i-1\) 点时的情况，即 \(d[i]=s[i]-s[i-1]=oil[i]-dist[i-1]\ge 0\)

由此可以推出，走到 \(i-x_{(0\le x\le n)}\) 点时，需要满足 \(s[i]-s[i-x]\ge 0\)。

从而转化为，在区间 \([i-n,i]\) 内找到最大值，满足 \(\max\{s[i-n,i]\}\le s[i]\)。寻找区间里最大值可以用滑动窗口来维护。

---

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 2000010;

int n;
int oil[N], dist[N], q[N];
LL s[N];
bool ans[N];

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    cin >> n;
    for (int i = 1; i <= n; i++) cin >> oil[i] >> dist[i];

    // 顺时针
    for (int i = 1; i <= n; i++) s[i] = s[i + n] = oil[i] - dist[i];
    for (int i = 1; i <= n * 2; i++) s[i] += s[i - 1];

    int hh = 0, tt = -1;
    for (int i = n * 2; i; i--) {
        if (hh <= tt && q[hh] > i + n) hh++;
        while (hh <= tt && s[q[tt]] >= s[i]) tt--;  
        q[++tt] = i; // s[i] 需要与 s[i - 1] 进行比较，所以先入队列
        if (i <= n && s[q[hh]] >= s[i - 1]) ans[i] = true;
    }

    // 逆时针
    dist[0] = dist[n];  // n~1点的距离
    for (int i = 1; i <= n; i++) s[i] = s[i + n] = oil[i] - dist[i - 1];
    for (int i = 1; i <= n * 2; i++) s[i] += s[i - 1];

    hh = 0, tt = -1;
    for (int i = 1; i <= n * 2; i++) {
        if (hh <= tt && q[hh] < i - n) hh++;
        if (i > n && s[q[hh]] <= s[i]) ans[i - n] = true;
        while (hh <= tt && s[q[tt]] <= s[i]) tt--;
        q[++tt] = i;
    }

    // 输出答案
    for (int i = 1; i <= n; i++) cout << (ans[i] ? "TAK" : "NIE") << endl;

    return 0;
}