任务安排 2

原题链接

题目描述

有 N 个任务排成一个序列在一台机器上等待执行，它们的顺序不得改变。

机器会把这 N 个任务分成若干批，每一批包含连续的若干个任务。

从时刻 0 开始，任务被分批加工，执行第 i 个任务所需的时间是 \(T_i\)。

另外，在每批任务开始前，机器需要 S 的启动时间，故执行一批任务所需的时间是启动时间 S 加上每个任务所需时间之和。

一个任务执行后，将在机器中稍作等待，直至该批任务全部执行完毕。

也就是说，同一批任务将在同一时刻完成。

每个任务的费用是它的完成时刻乘以一个费用系数 \(C_i\)。

请为机器规划一个分组方案，使得总费用最小。

思路推式子+斜率优化DP

本题与任务安排 1(时间复杂度 \(O(n^2)\)) 相同，仅数据范围不同。本题 \(1\le n\le 3\times 10^5\)，需要在 \(O(n)\) 的时间复杂度内得出答案。

上题得到的朴素版dp状态转移方程：

\[dp[i]=\min\{dp[j]+t[i]\times(c[i]-c[j])+S\times(c[n]-c[j])\}_{(0\le j\le i-1)}\]

将上式括号拆开可得出：

\[dp[i]=\min\{dp[j]+t[i]\times c[i]-t[i]\times c[j]+S\times c[n]-S\times c[j]\}_{(0\le j\le i-1)}\]

提出式中单独含有 \(i\) 的常量：

\[dp[i]=t[i]\times c[i]+S\times c[n]+\min\{dp[j]-c[j]\times(t[i]+S)\}_{(0\le j\le i-1)}\]

观察式子 \(\min\{dp[j]-c[j]\times(t[i]+S)\}_{(0\le j\le i-1)}\)

可以发现该多项式可以抽象成 \(变量1-变量2\times(常量i+常量S)\)

对于 变量1 \(dp[j]\) 可以发现是与 \(j\) 有关的变量；
对于 变量2 \(c[j]\) 可以发现也是与 \(j\) 有关的变量。

因此，不妨令 \(\begin{cases} y(j)=dp[j] \\ x(j)=c[j] \\ k_i=t[i]+S \end{cases}\) ，则该函数可视为 \(y(j)-x(j)\times k\)

以下为了方便阅读，把 \(y(j)\) 简写为 \(y\)，\(x(j)\) 简写为 \(x\)。

求函数 \(y-kx_{(0\le j\le i-1)}\) 的极值，可以使用直线的斜截式方程：\(y=kx+b\)。

对直线斜截式方程进行变形：\(b=y-kx\)。

要求函数 \(y-kx\) 的极值，即求一个点 \((x_j,y_j)\) 与当前斜率 \(k_i\) 构成的所有直线中，y轴截距最小。

数缺形时少直观，形少数时难入微，数形结合百般好。 —— 华罗庚

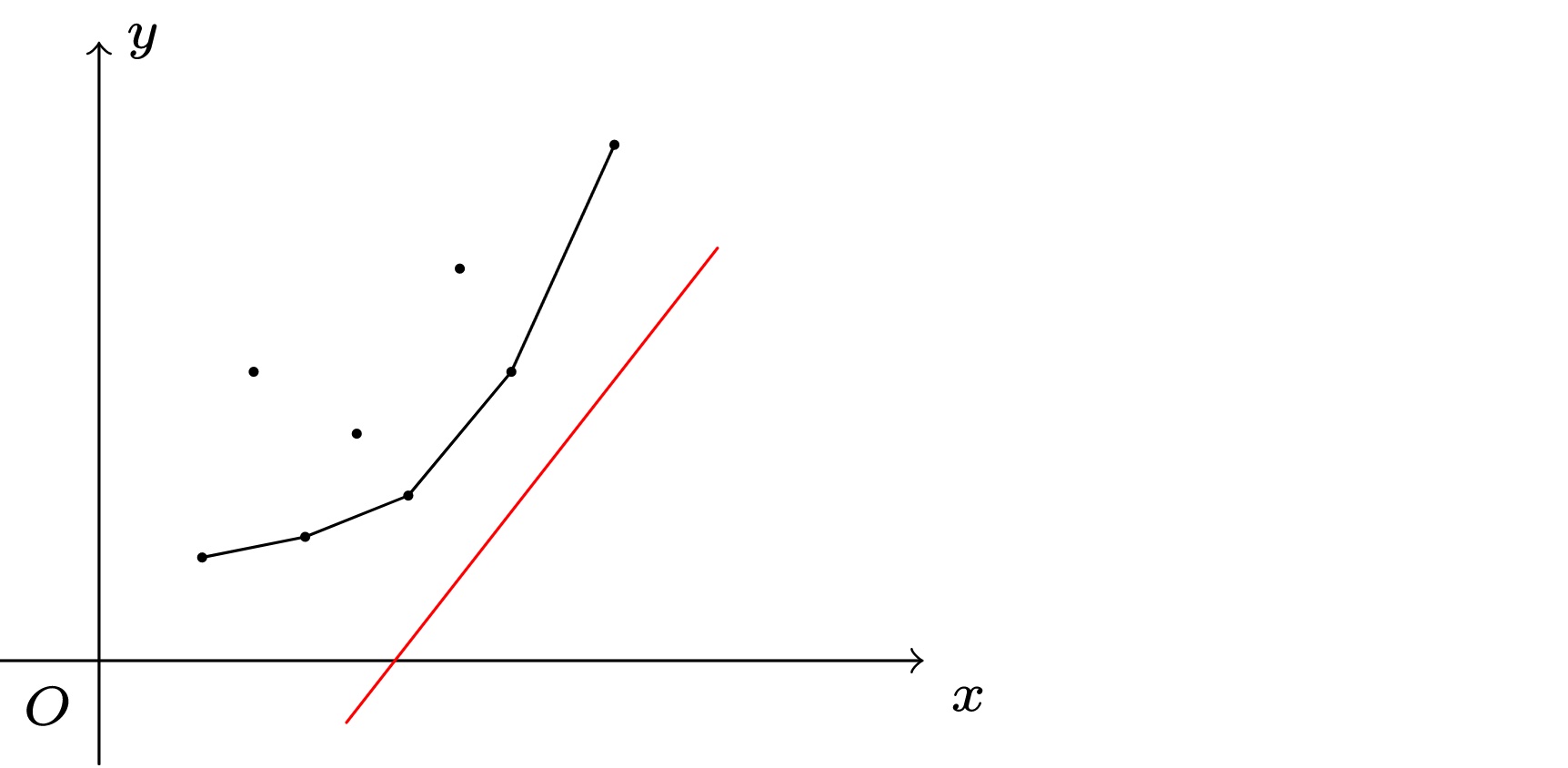
图中，黑色点为所有 \(0≤j<i\) 的点 \((x_j,y_j)\)，红色线为斜率是 \(k_i\) 的某一条直线。

我们从下往上（截距从小到大）去逼近当前所有的点则第一个出现在直线上的点，就是满足 \(b_i=y_j−kx_j\) 的最小截距 \(b_i\)，即是当前阶段 DP 的最佳策略。

如何有效维护一个点集？

这就是一个 线性规划 的问题了：在点集中，找到一个点，绘制 固定斜率 的直线，使得 截距最小。

由 线性规划 知识可知：我们只用考虑点集中凸壳上的点即可。

几何直观上，显然这题要维护的是 下凸壳。

因此，对于任意的 \(dp_i\) 来说，我们只需去寻找下凸壳上的点构成直线的最小截距即可。

但是在最坏的情况下，点集的数量最大也会达到 \(O(n)\)。（即全部的点构成了一个下凸壳）

观察直线方程：\(\min\{dp[j]-c[j]\times(t[i]+S)\}_{(0\le j\le i-1)}\)，由于 \(t_i,c_i\) 都是正整数，因此它们的前缀和 \(t[i],c[i]\) 是单调递增的。

对应直线方程的参数，即 \(x(j)=c[j]\) 与 \(k=t[i]+S\) 皆为单调递增，而下凸壳相邻两点之间的斜率也是单调递增的。

则下凸壳中第一个出现在直线上的点，满足：\(k_{j−1,j}≤k_i<k_{j,j+1}\)，此时直线截距 \(b_j\) 最小。如下图所示：

而又由于 \(k_i\) 单调递增，所以 \(j\) 之前的点都不会是点集中出现在直线上的第一个点。

此时只需维护点集区间 \([j,i]\) 的点即可，直到 \(k_{j,j+1}≤k<k_{j+1,j+2}\) 时，维护点集区间变为 \([j+1,i]\)。

故可以使用单调队列来维护下凸壳的有效点集。

查询时，队头小于当前斜率上的点全删。即用队头的两个元素维护大于当前斜率 \(k_i\) 的最小斜率 \(k_{q[hh] , q[hh+1]}\)。

\[\dfrac{dp_{q[hh+1]}-dp_{q[hh]}}{c_{q[hh+1]}-c_{q[hh]}}\le t_i+S\]

插入时，队尾不在凸包上的点全删。队列中至少有两个点，然后把满足 \(k_{q[tt−1],q[tt]}≥k_{q[tt] , i}\) 的点 \(q[tt]\) 弹出。即新加入的点，必须和原点集构成下凸壳，无效点要先删去。

\[\dfrac{dp_{q[tt]}-dp_{q[tt-1]}}{c_{q[tt]}-c_{q[tt-1]}}\ge\dfrac{dp_i-dp_{q[tt]}}{c_i-c_{q[tt]}}\]

上式变形，即为：

查询： \(dp_{q[hh+1]}-dp_{q[hh]}\le (t_i+S)\times (c_{q[hh+1]}-c_{q[hh]})\)
求解： \(dp_i=t_i\times c_i+S\times c_n+dp_j-c_j\times(t_i+S)\)
插入： \((dp_{q[tt]}-dp_{q[tt-1]})\times(c_i-c_{q[tt]})\ge(dp_i-dp_{q[tt]})\times(c_{q[tt]}-c_{q[tt-1]})\)

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 300010;

int n, s;
LL t[N], c[N], dp[N], q[N];
// dp[i]: 前 i 个任务分配的最小费用方案

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    cin >> n >> s;
    for (int i = 1; i <= n; i++) {
        cin >> t[i] >> c[i];
        t[i] += t[i - 1];
        c[i] += c[i - 1];
    }

    int hh = 0, tt = 0;
    for (int i = 1; i <= n; i++) {
        // 1. hh < tt: 两点确定一个斜率
        // 2. 查询时，队头小于当前斜率点全删
        // 3. 插入时，队尾不在凸包上的点全删

        // query
        while (hh < tt && dp[q[hh + 1]] - dp[q[hh]] <= (t[i] + s) * (c[q[hh + 1]] - c[q[hh]])) hh++;
        int j = q[hh];  // 得到满足当前斜率的点

        // get answer
        dp[i] = t[i] * c[i] + s * c[n] + dp[j] - c[j] * (t[i] + s);

        // insert
        while (hh < tt && (dp[q[tt]] - dp[q[tt - 1]]) * (c[i] - c[q[tt]]) >= 
                (dp[i] - dp[q[tt]]) * (c[q[tt]] - c[q[tt - 1]])) tt--;
        q[++tt] = i;
    }

    cout << dp[n] << endl;

    return 0;
}

任务安排 2

题目描述

思路 推式子+斜率优化DP

代码

思路推式子+斜率优化DP