传纸条

原题链接

小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。

一次素质拓展活动中，班上同学安排坐成一个 m 行 n 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。

幸运的是，他们可以通过传纸条来进行交流。

纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标 (1,1)，小轩坐在矩阵的右下角，坐标 (m,n)。

从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。

在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。

班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙，反之亦然。

还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 0 表示），可以用一个 0∼100 的自然数来表示，数越大表示越好心。

小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。

现在，请你帮助小渊和小轩找到这样的两条路径。

输入格式

第一行有 2 个用空格隔开的整数 m 和 n，表示学生矩阵有 m 行 n 列。

接下来的 m 行是一个 m×n 的矩阵，矩阵中第 i 行 j 列的整数表示坐在第 i 行 j 列的学生的好心程度，每行的 n 个整数之间用空格隔开。

输出格式

输出一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。

数据范围

\(1≤n,m≤50\)

输入样例：

输出样例：

证明

首先，从右下角回传可以等价为从左上角同时传两次。要想两个路径除了起点和终点之外没有交点，那么肯定有一条路径完全位于另一条的上方。现在考虑路径有交点的情况：

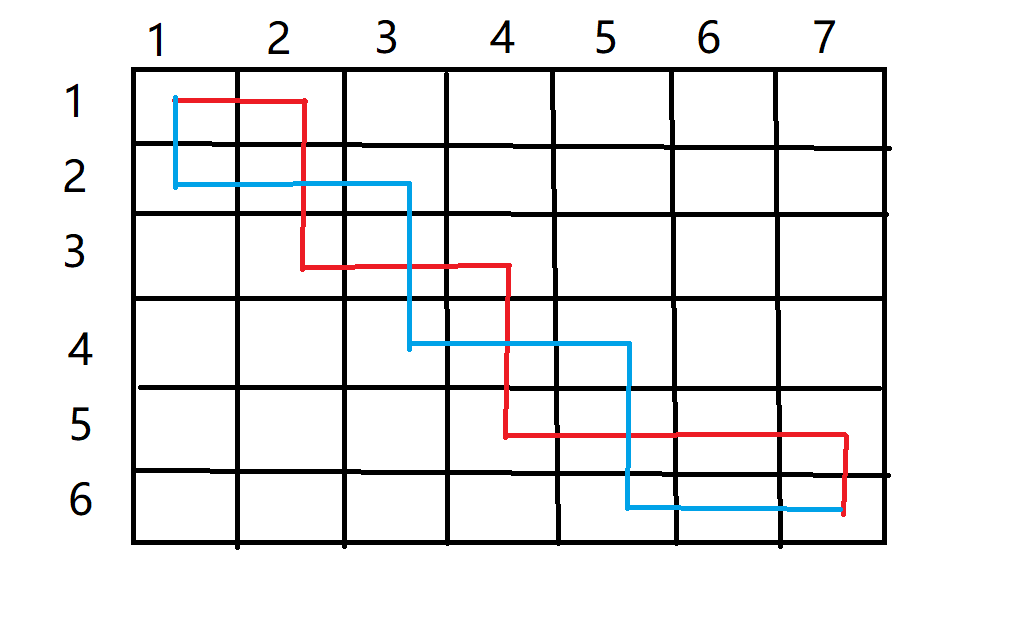
这种情况其实转换起来很简单，只要把位于红色线段上方的蓝色线段交换颜色就可以了，也就是说当红色处于蓝色的下方的时候，将红色的路径换成从蓝色的那段走是等效的（因为两条路径加起来经过的节点完全没有变）。

就可以得到：

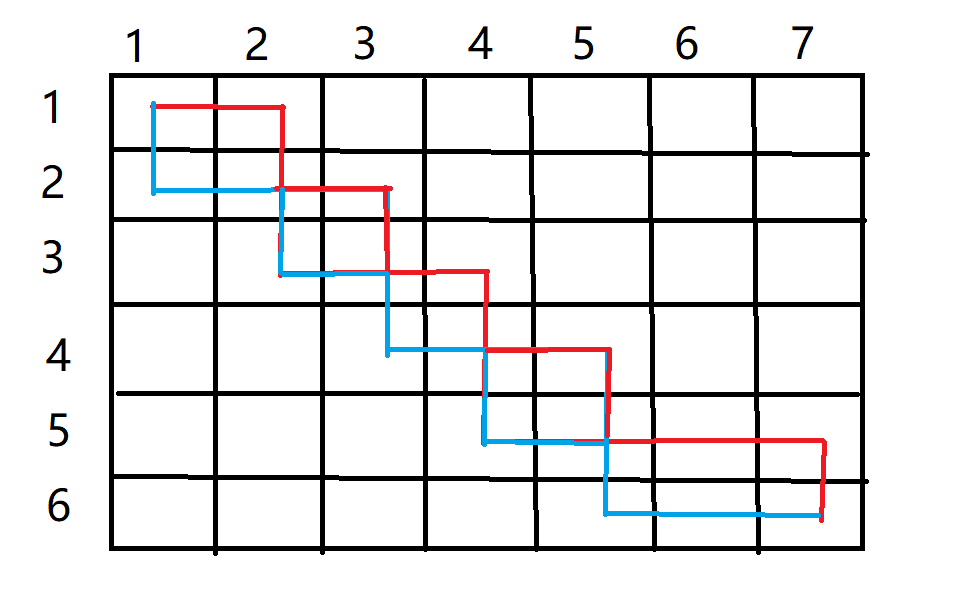
但是这个时候虽然满足了红色路径完全在蓝色的上方，但是却有交点。但是因为所有节点的权值都为非负数，那么可以证明这种情况永远不可能是最优解。比如以交点（2，2）为例，蓝色从（3，1）绕道或者红色从（1，3）处绕道一定不会比两条路径都从（2，2）处走差。

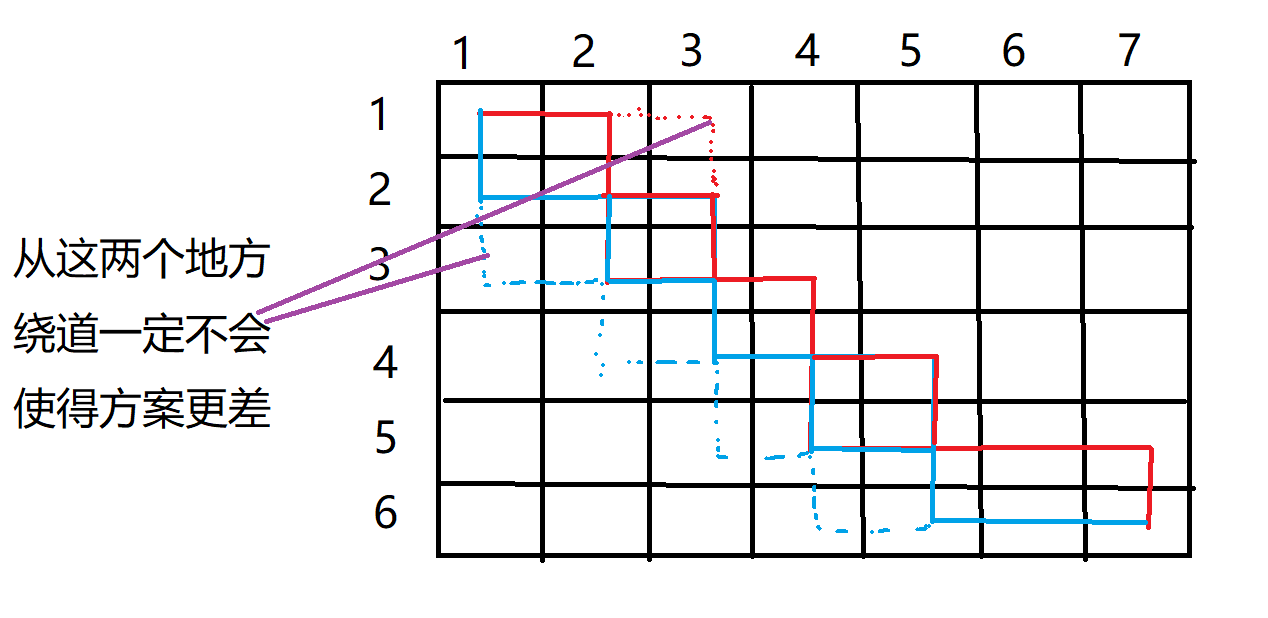
绕过交点之后，可以得到蓝色虚线的方案，该方案一定不会比之前的两个实线的方案更差。（当然该方案也不一定是最优的，还要确定应该由蓝色还是红色来走原来的交点的位置。

因此，最优解永远不会是两条相交的线路

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 55;

int n, m;
int w[N][N];
int dp[N << 1][N][N];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> w[i][j];

    for (int k = 2; k <= n + m; k++)
        for (int i1 = 1; i1 <= n; i1++)
            for (int i2 = 1; i2 <= n; i2++) {
                int j1 = k - i1, j2 = k - i2;
                if (j1 >= 1 && j1 <= m && j2 >= 1 && j2 <= m) {
                    int t = w[i1][j1];
                    if (i1 != i2) t += w[i2][j2];

                    int &x = dp[k][i1][i2];
                    x = max(x, dp[k - 1][i1][i2] + t);
                    x = max(x, dp[k - 1][i1 - 1][i2] + t);
                    x = max(x, dp[k - 1][i1][i2 - 1] + t);
                    x = max(x, dp[k - 1][i1 - 1][i2 - 1] + t);
                }
            }

    cout << dp[n + m][n][n] << endl;

    return 0;
}