观光之旅
原题链接
题目描述
给定一张无向图,求图中一个至少包含 3 个点的环,环上的节点不重复,并且环上的边的长度之和最小。
该问题称为无向图的最小环问题。
你需要输出最小环的方案,若最小环不唯一,输出任意一个均可。
思路
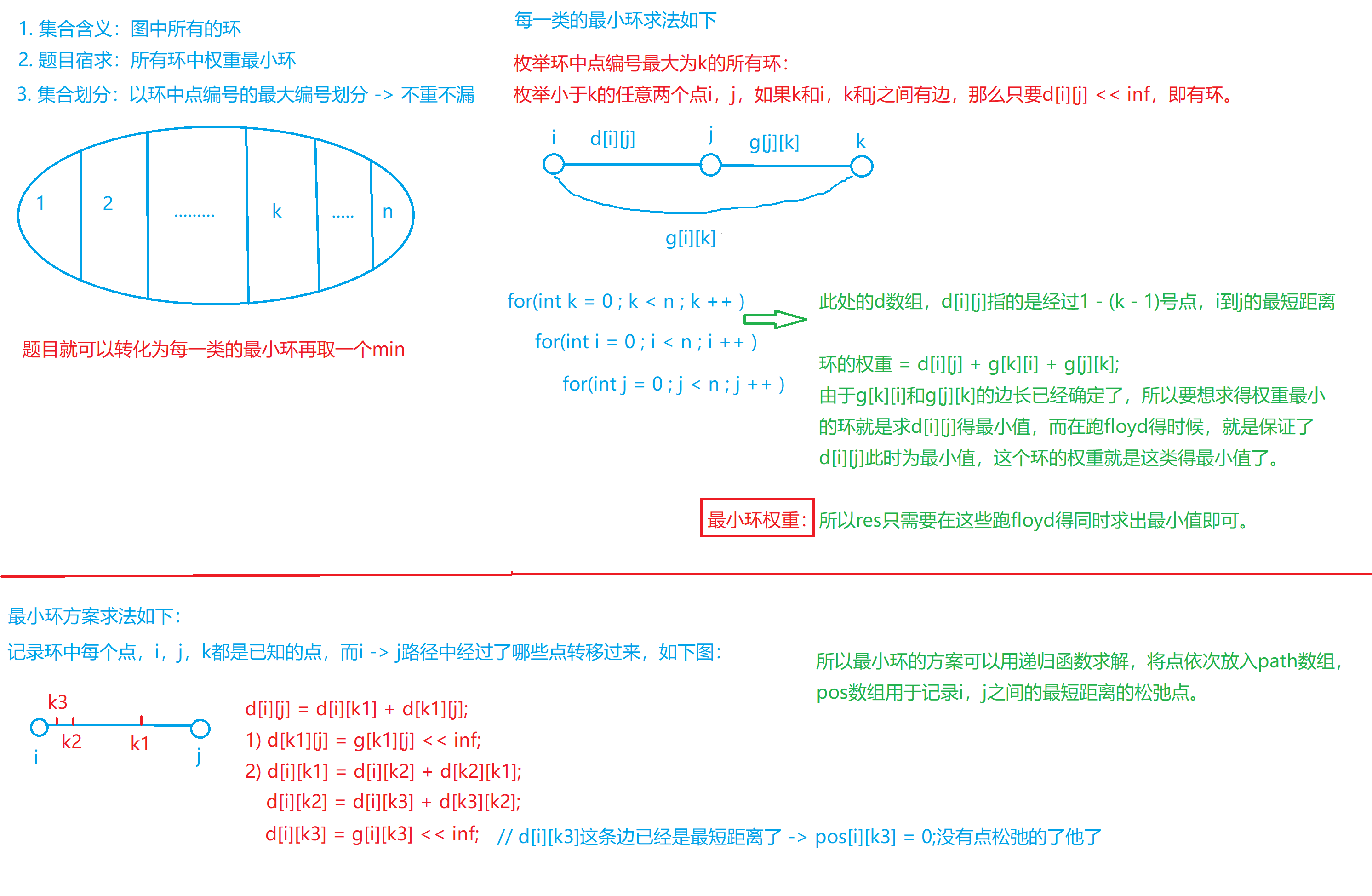
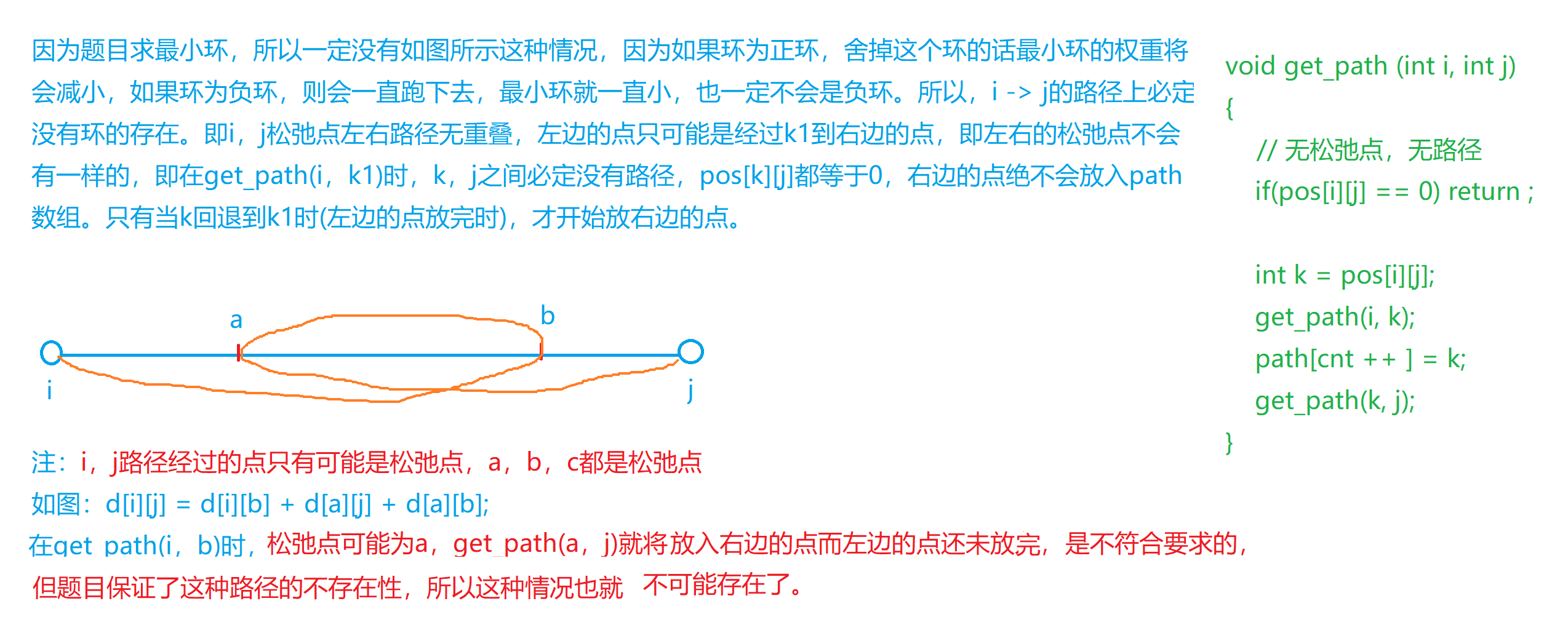
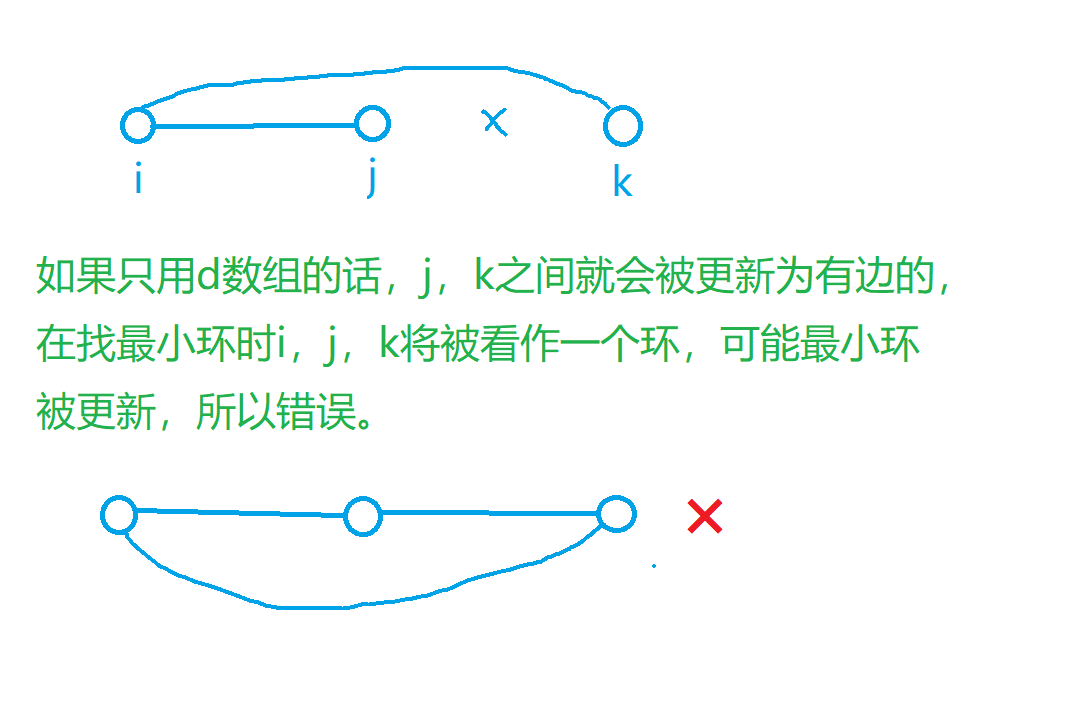
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66 | #include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 110;
const int inf = 0x3f3f3f3f;
int n, m, cnt;
int d[N][N], g[N][N];
int p[N][N], path[N];
void get_path(int i, int j) {
if (p[i][j] == 0) return;
int k = p[i][j];
get_path(i, k);
path[cnt++] = k;
get_path(k, j);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> m;
memset(g, 0x3f, sizeof g);
for (int i = 1; i <= n; i++) g[i][i] = 0;
while (m--) {
int a, b, c;
cin >> a >> b >> c;
g[a][b] = g[b][a] = min(g[a][b], c);
}
int res = inf;
memcpy(d, g, sizeof d);
for (int k = 1; k <= n; k++) {
for (int i = 1; i < k; i++)
for (int j = i + 1; j < k; j++) {
if ((LL)d[i][j] + g[j][k] + g[k][i] < res) {
res = d[i][j] + g[j][k] + g[k][i];
cnt = 0;
path[cnt++] = k;
path[cnt++] = i;
get_path(i, j);
path[cnt++] = j;
}
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (d[i][j] > d[i][k] + d[k][j]) {
d[i][j] = d[i][k] + d[k][j];
p[i][j] = k;
}
}
if (res == inf) cout << "No solution." << endl;
else {
for (int i = 0; i < cnt; i++) cout << path[i] << ' ';
cout << endl;
}
return 0;
}
|


