最短路计数

原题链接

题目描述

给出一个 N 个顶点 M 条边的无向无权图，顶点编号为 1 到 N。

问从顶点 1 开始，到其他每个点的最短路有几条。

---

思路

要求最短路计数首先满足条件是不能存在值为0的环，因为存在的话那么被更新的点的条数就为INF了。 要把图抽象成一种最短路树（拓扑图）。

BFS 只入队一次，出队一次。可以抽象成拓扑图， 因为它可以保证被更新的点的父节点一定已经是最短距离了，并且这个点的条数已经被完全更新过了。这个性质是核心性质。

dijkstra 每个点只出队一次。也可以抽象成拓扑图， 同理由于每一个出队的点一定已经是最短距离，并且它出队的时候是队列中距离最小的点，这就代表他的最短距离条数已经被完全更新了，所以构成拓扑性质。

bellman_ford算法 spfa 本身不具备拓扑序，因为更新它的点不一定是最短距离，所以会出错。

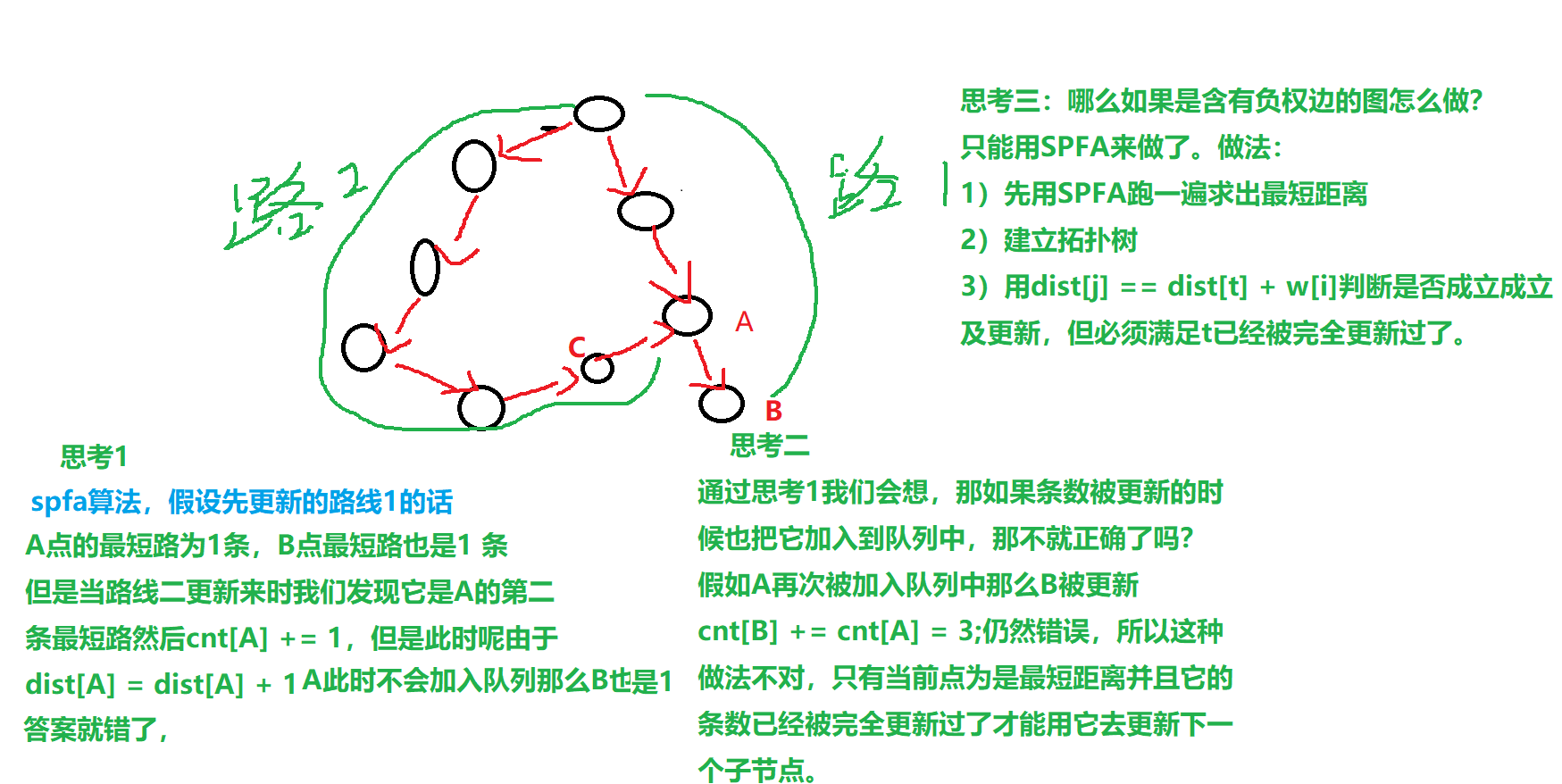
但如果图中存在负权边只能用该算法做，也能做但是比较麻烦

先跑一遍spfa找到每个点的最短距离,把最短路拓扑树建立出来，看哪一条边 dist[j] == dist[t] + w[i],然后更新它。

代码 BFS

#include <bits/stdc++.h>
using namespace std;

const int N = 100010, M = 400010;
const int mod = 100003;

int n, m;
int h[N], e[M], ne[M], idx;
int dist[N], cnt[N];

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    cnt[1] = 1;

    queue<int> q;
    q.push(1);

    while (!q.empty()) {
        int t = q.front();
        q.pop();

        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[t] + 1) {
                dist[j] = dist[t] + 1;
                cnt[j] = cnt[t];
                q.push(j);
            } else if (dist[j] == dist[t] + 1) {
                cnt[j] = (cnt[j] + cnt[t]) % mod;
            }
        }
    }
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    memset(h, -1, sizeof h);
    cin >> n >> m;
    while (m--) {
        int a, b;
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }

    bfs();

    for (int i = 1; i <= n; i++) cout << cnt[i] << endl;

    return 0;
}