跳转至

观光

原题链接

题目描述

“您的个人假期”旅行社组织了一次比荷卢经济联盟的巴士之旅。

比荷卢经济联盟有很多公交线路。

每天公共汽车都会从一座城市开往另一座城市。

沿途汽车可能会在一些城市（零或更多）停靠。

旅行社计划旅途从 S 城市出发，到 F 城市结束。

由于不同旅客的景点偏好不同，所以为了迎合更多旅客，旅行社将为客户提供多种不同线路。

游客可以选择的行进路线有所限制，要么满足所选路线总路程为 S 到 F 的最小路程，要么满足所选路线总路程仅比最小路程多一个单位长度。

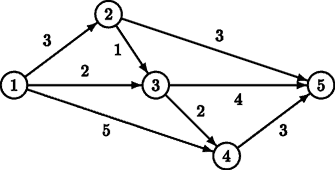
如上图所示，如果 S=1，F=5，则这里有两条最短路线 1→2→5,1→3→5，长度为 6；有一条比最短路程多一个单位长度的路线 1→3→4→5，长度为 7。

现在给定比荷卢经济联盟的公交路线图以及两个城市 S 和 F，请你求出旅行社最多可以为旅客提供多少种不同的满足限制条件的线路。

思路 Dijkstra

  1. 设状态 \(dist[i][0,1]\) 表示初始城市 \(S\) 到城市 \(i\) 的最短距离和次短距离，\(cnt[i][0,1]\) 表示城市SS到城市ii的最短路径和次短路经的条数
  2. 初始时，\(dist[S][0]\) 为 \(0\)，\(cnt[S][0]\) 为 \(1\)（其余都初始化成正无穷，初始时S不存在次短路）

  3. Dijkstra算法枚举城市 \(v\) 可通往的城市 \(j\) 时，有四种情况：

    • \(dist[j][0]>dist[v][type]+w[i]\)：当前最短路变成次短路，更新最短路，将最短路和次短路加入优先队列
    • \(dist[j][0]=dist[v][type]+w[i]\)：找到一条新的最短路，更新最短路条数
    • \(dist[j][1]>dist[v][type]+w[i]\)：找到一条更短的次短路，覆盖掉当前次短路，加入优先队列
    • \(dist[j][1]=dist[v][type]+w[i]\)：找到一条新的次短路，更新次短路条数

  4. 到 \(F\) 城市的次短路径如果比最短路径恰好多 \(1\)，则把这样的路径条数加到答案里

  5. C++ 优先队列大根堆需要重载小于号，小根堆需要重载大于号

时间复杂度 \(O(m\log n)\)

代码

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
#include <bits/stdc++.h>
using namespace std;

const int N = 1010, M = 10010;

int n, m, S, F;
int h[N], e[M], w[M], ne[M], idx;
int dist[N][2], cnt[N][2];
bool st[N][2];

struct node {
    int ver, dist, type;
    bool operator > (const node &t) const {
        return dist > t.dist;
    }
};

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int dijkstra() {
    memset(dist, 0x3f, sizeof dist);
    memset(st, false, sizeof st);
    memset(cnt, 0, sizeof cnt);

    dist[S][0] = 0;
    cnt[S][0] = 1;

    priority_queue<node, vector<node>, greater<node>> q;
    q.push({S, 0, 0});

    while (!q.empty()) {
        auto [ver, distence, type] = q.top();
        q.pop();

        if (st[ver][type]) continue;
        st[ver][type] = true;

        for (int i = h[ver]; i != -1; i = ne[i]) {
            int j = e[i];
            if (dist[j][0] > distence + w[i]) {
                // 修改次短路
                dist[j][1] = dist[j][0];
                cnt[j][1] = cnt[j][0];
                q.push({j, dist[j][1], 1});

                // 修改最短路
                dist[j][0] = distence + w[i];
                cnt[j][0] = cnt[ver][type];
                q.push({j, dist[j][0], 0});
            } else if (dist[j][0] == distence + w[i]) {
                // 存在与最短路相同的路径
                cnt[j][0] += cnt[ver][type];
            } else if (dist[j][1] > distence + w[i]) {
                // 修改次短路
                dist[j][1] = distence + w[i];
                cnt[j][1] = cnt[ver][type];
                q.push({j, dist[j][1], 1});
            } else if (dist[j][1] == distence + w[i]) {
                // 存在与次短路相同的路径
                cnt[j][1] += cnt[ver][type];
            }
        }
    }

    int res = cnt[F][0];
    if (dist[F][1] == dist[F][0] + 1) res += cnt[F][1];

    return res;
}

void solve() {
    memset(h, -1, sizeof h);
    idx = 0;

    cin >> n >> m;
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }

    cin >> S >> F;

    cout << dijkstra() << endl;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int T;
    cin >> T;
    while (T--) {
        solve();
    }

    return 0;
}
回到页面顶部