车站分级

原题链接

题目描述

一条单向的铁路线上，依次有编号为 1, 2, …, n 的 n 个火车站。

每个火车站都有一个级别，最低为 1 级。

现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 x，则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点） 

例如，下表是 5 趟车次的运行情况。

其中，前 4 趟车次均满足要求，而第 5 趟车次由于停靠了 3 号火车站（2 级）却未停靠途经的 6 号火车站（亦为 2 级）而不满足要求。

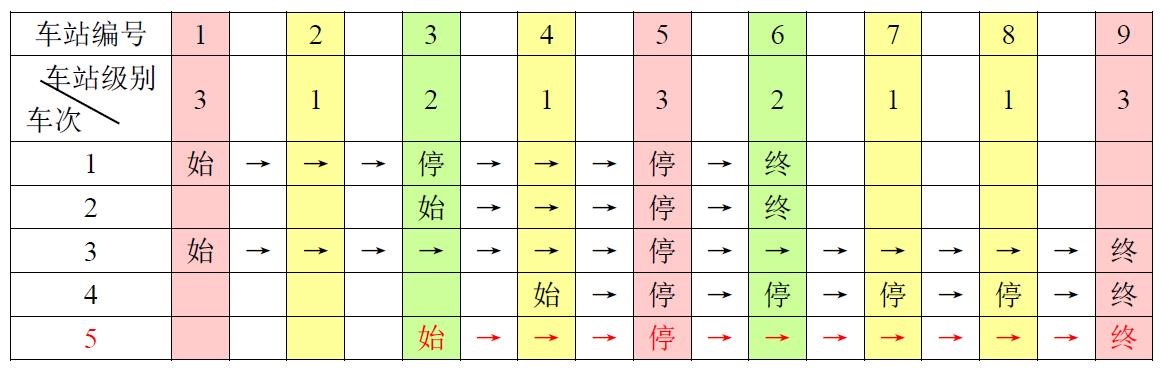
现有 m 趟车次的运行情况（全部满足要求），试推算这 n 个火车站至少分为几个不同的级别。

---

拓扑排序+虚拟点+最长路

dist[i]：表示i点在拓扑图中离起点的最远距离(可能存在多起点)，dist[起点] == 1,边的权值为1

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 2010, M = 1000010;

int n, m;
int h[N], e[M], w[M], ne[M], idx;
int d[N], dist[N];
bool st[N];
vector<int> v;

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++, d[b]++;
}

void topsort() {
    queue<int> q;
    for (int i = 1; i <= n + m; i++)
        if (!d[i])
            q.push(i);

    while (q.size()) {
        int u = q.front();
        q.pop();

        v.push_back(u);

        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (--d[j] == 0) q.push(j);
        }
    }
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        memset(st, false, sizeof st);
        int cnt;
        cin >> cnt;
        int start = n, end = 1;
        while (cnt--) {
            int stop;
            cin >> stop;
            st[stop] = true;
            start = min(start, stop);
            end = max(end, stop);
        }

        int ver = n + i;
        for (int j = start; j <= end; j++) {
            if (!st[j]) add(j, ver, 0);
            else add(ver, j, 1);
        }
    }

    topsort();

    for (int i = 1; i <= n; i++) dist[i] = 1;
    for (int i = 0; i < n + m; i++) {
        int j = v[i];
        for (int k = h[j]; k != -1; k = ne[k])
            dist[e[k]] = max(dist[e[k]], dist[j] + w[k]);
    }

    int res = 0;
    for (int i = 1; i <= n; i++) res = max(res, dist[i]);
    cout << res << endl;

    return 0;
}